On a donc pour tout n
IN1°) Définition
Une suite u dont aucun terme n'est nul est géométrique si le rapport entre deux termes consécutifs est constant. Cette constante q est alors appelé raison de la suite.
On a donc pour tout nIN
= q ou un+1 =un xq
On passe d’un terme au suivant en multipliant toujours par le même nombre q.
Exemple :
La suite u n définie
pour tout n
IN ,
définie par
u n = 3n est-elle géométrique ?
Pour répondre à cette question, on calcule le quotient
Ce quotient est constamment égal à 3, la suite est donc géométrique de raison 3.
Exemple :
La suite (u n ) définie
pour tout n
IN,
par u n = n2 +1est-elle géométrique ?
Comme cette suite n’est jamais nulle, pour répondre à cette question, on calcule le quotient
Ce quotient dépend de n.
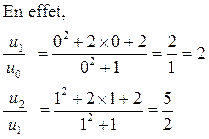
La suite n’est donc pas géométrique.
Méthode :
Pour tester si une suite est géométrique, on calcule (après avoir vérifié qu’aucun terme ne s’annule) le quotient entre deux termes consécutifs. Si ce quotient est constant, la suite est géométrique de raison cette constante.
2°) Calcul du terme général
(u n ) étant une suite géométrique de raison q, on a :
u 1 =u 0 xq
u2 =u 1 x q=(u 0 xq)xq=u 0 xq2
u3 =u 2 x q=(u 0 xq2)xq=u 0 xq3
.....
(un
) étant une suite géométrique, pour tout n
IN on
a un = u0 x qn
Exercice :
On considère la suite (u n ) géométrique de premier terme u0= 2 et de raison 5.
Calculer u10
On calcule
u 1 =u 0 x=2x5=10
u2 =u 1 x 5=(u 0 x5)x5=2 x52=50
u3 =u 2 x 5=(u 0 x52)xq=u 0 x53=250
u4 =u 3 x 5=(u 0 x53)x5=u 0 x54=1250
On conjecture (on devine sans démonstration) alors que un+1= u0x5n.
Cette expression nous permet alors « facilement » de calculer u10= u0x510 = 19531250
Propriété
Si u est une suite géométrique de raison q et de premier terme u alors pour tout n IN: u n= u 0 x qn.
Réciproquement
Si une suite est définie par u n= a x rn alors elle est gémétrique de raison r et de premier terme a
Démonstration
Nous allons montrer cette propriété par récurrence.
On note P(n) la propriété un= u0 x qn
1. On calcule u0xq0=u0 La propriété P(0) est donc vraie.
2. On suppose que P(n) est vraie pour un certain n.
On calcule alors : un+1= un x q = u0 x qn x q = u0 x qn+1
La propriété P(n+1) est donc aussi vraie.
3. On a donc montré par récurrence que la propriété est vraie pour tout n. P(n)
Application :
On considère la suite un géométrique de premier terme u0= 2et de raison 10.
Calculer u15
D'aprés la propriété u15=2x1015= 2 000 000 000 000 000
3°) Somme de termes consécutifs
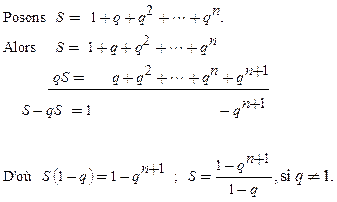
Si 
,
· Le résultat s’étend à une somme de termes consécutifs à partir d’un rang quelconque:
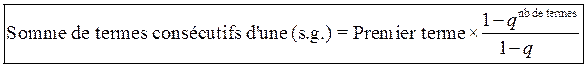
On admettra (sans démonstration) plus généralement,
Propriété
Si u est une suite géométrique de premier terme a et de raison r alors
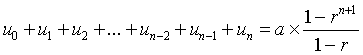
Démonstration :
S n= u 0 + u 1 + u2 + u3 ..........+u n-1 + u n
=a x r0+a x r1+a x r2+............a x rn-1+a x rn
=a(1+r1+r2+............rn-1+rn)
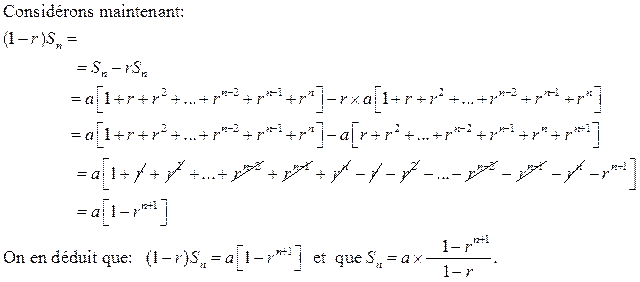
Exercice :
Calculer 1+2+4+8+16+32+64+128+256+512+1024 sans poser d'opération.
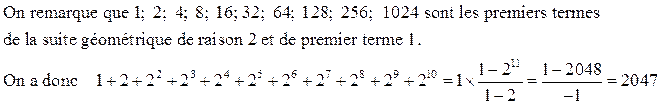
Rem : Moyenne géométrique
Si a , b et c sont trois termes consécutifs d’une suite géométrique alors b ² = a c .
Si trois nombres positifs a , b et c vérifient b ² = a c , on dit que b est la moyenne géométrique de a et c .